Understanding Confidence Intervals in Heat Loss Measurements and Calculations

What’s the Difference between a Heat Loss Measurement and a Heat Loss Calculation?

Heat loss measurements use real-world data to quantify heat loss. There are minor methodological differences, but broadly this involves measuring the rate of heat inputs (energy consumption) and the internal-external temperature difference to infer the rate of heat loss per degree (the Heat Transfer Coefficient or HTC). Heat loss measurements are not informed by what the building construction methods or materials are, rather they are a direct measurement of its performance.

Heat loss calculations are carried out by summing each heat loss element of a building. For fabric heat loss this means multiplying the area of each part of the building by its U-value, with the U-value sourced from a lookup table or calculation, and then adding in thermal bridges by a simple assumption or detailed calculations. For infiltration, the heat loss calculation estimates the amount of air movement based on an assumption or measurement of airtightness, with a similar further calculation for ventilation flow rates and associated heat transfer.

What Is a Confidence Interval?

A confidence interval defines a boundary within which we can be reasonably certain the true value lies. In most cases, a 95% confidence interval is used, meaning that we can be 95% confident that the correct answer is within this range. This statistical approach acknowledges the inherent variability and limitations in data collection and analysis.

Within the given confidence interval, the reported result is the most likely correct answer.

Factors Influencing Heat Loss Measurements Confidence Interval Size

The size of the confidence interval for heat loss measurements is influenced by a myriad of factors, such as:

• Sensor and data collection uncertainty for key parameters like temperature, energy, and weather
• Heat transfer to and from neighbours through party walls, floors, and ceilings
• The efficiency of heating and ventilation systems
• Contributions from metabolic heat generated by occupants and heat gains from sunlight

Each of these factors contributes to the overall uncertainty in heat loss measurements, ultimately affecting the width of the confidence interval.

Repeatability in a Single Building

Repeatability - the ability to obtain consistent results when measuring the same building under similar conditions - tends to be much better than the given confidence interval. This is because several sources of uncertainty remain constant within a single building. As a result, even if the confidence interval is broad, it reflects broader uncertainties rather than inconsistencies in measurement.

Uncertainty in Heat Loss Calculations

Despite its importance, it is almost unheard of for confidence intervals to be calculated and reported for heat loss calculations. However, that uncertainty does exist. For heat loss calculations the problem is that these calculations are informed by a visual survey and assumed values for key inputs. Things like airtightness, whether there is insulation in a cavity and if it is well installed, and how well the insulation under the floor and in the walls join up are impossible to determine by a visual survey. However, measurements show that even within a particular construction type, in-situ performance varies by 100% or more.

For example, in a BRE study of more than 300 solid walls, the average U-value was 1.6W/m2K but the range of results was more than 2W/m2K. In this case, even within a narrow definition of a particular wall type, the range in performance was greater than the average. In plain speak, this means that the performance of seemingly similar walls, floors, and roofs vary widely such that you can’t accurately represent them with a single figure for an archetype.

When you use an assumption based on an archetype as an input to a heat loss calculation, like RdSAP or BS12831, you introduce that possible error (or uncertainty) in that input to the result. The uncertainty in the reliability of assessing input values applies to all of the U-values, airtightness, ventilation and thermal bridging which are not measured in-situ. If these were summed then the resulting confidence interval in the final output would be very high, with the amount varying for each calculation depending on the details of the building and how detailed the knowledge of the inputs is. To indicate the size of the uncertainty in calculation results, errors of 100% and more have been found regularly (see great research on this topic here & here).

Comparing Heat Loss Measurements to Traditional Calculation Methods

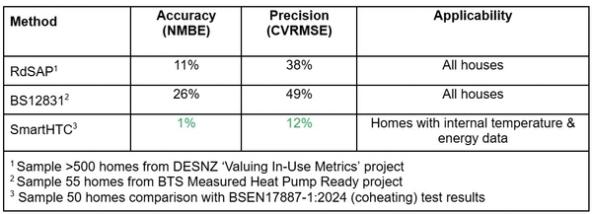
Although confidence intervals for heat loss measurements can seem offputting, it’s essential to understand them in context. Compared to traditional heat loss calculation methods, such as BS12831 or RdSAP a SmartHTC heat loss measurement has:

• Higher Accuracy: Heat loss measurements had 26 times less bias toward over- or under-sizing heat loss than BS12831 calculations
• Better Precision: Measurements provided results 3 times more closely grouped around the correct answer than BS12831 calculations

This improved accuracy and precision mean that, if properly calculated and reported, the confidence interval for a heat loss measurement is much narrower and more reliable than that of traditional heat loss calculations.